idealgogl.blogg.se - Name an altitude geometry

NAME AN ALTITUDE GEOMETRY HOW TO

The given angles of a triangle ABC are in the ratio of 1 : 2 : 3. Medians and Altitudes of Triangles Examples The Median, and altitude of the isosceles triangle are the same.Altitude, median, angle bisector interchange in case of an isosceles triangle.The Median, angle bisector is the same in an isosceles triangle when the altitude is drawn from the vertex to the base.The median and altitude of an isosceles triangle have some particular features. Isosceles Triangle is a type of triangle that has two sides or angles of equal measurement. Median and Altitude of an Isosceles Triangle The altitude of a triangle may lie inside or outside the triangle.Here O is called the ortho-center of triangle ABC. The point of intersection of three altitudes is called the ortho-center of the triangle.

Three altitudes always meet at a single point.

An altitude is also called the shortest distance from the vertex to the opposite side of a triangle.

Here AD, BE, CF are the altitudes of the triangle ABC. The altitude is a straight line that starts from the triangle vertex and stretches till the opposite side of the vertex making a right angle with the side of the triangle.

So, 3 medians divide a triangle into 6 smaller triangles of equal area.

Each median of a triangle divides the triangle into two smaller triangles having the same area.

The point where 3 medians meet is called the centroid of the triangle.

The three medians meet at a single point.

Here AD, BE, CF are the 3 medians of the triangle ABC.

All triangles have 3 medians, each one from the triangle vertex.

In △ ABC, AD is the median that divides a side BC into two equal parts. A triangle can have a maximum of three medians and the point of intersection of three medians is called the center of the triangle. Median in a triangle is nothing but the straight line that joins one vertex and midpoint of the side that is opposite to the vertex.

The triangle on the Same Base and between Same Parallels Theorem.

Here, we will learn more about the Medians and Altitudes of a Triangle. Both median, altitude is the lines in the triangle. And based on the angle measurement, triangles are again classified into three various types they are right, acute, oblique triangles. Depending on the side length triangles are divided into three types they are equilateral triangle, isosceles triangle, and scalene triangle. The sum of interior angles of a triangle is 180 degrees.

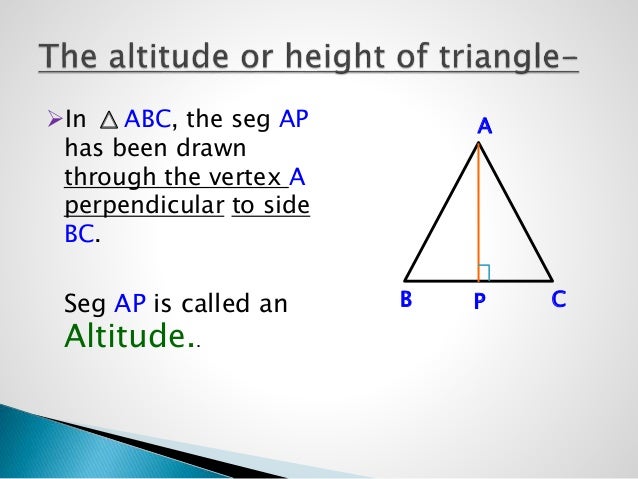
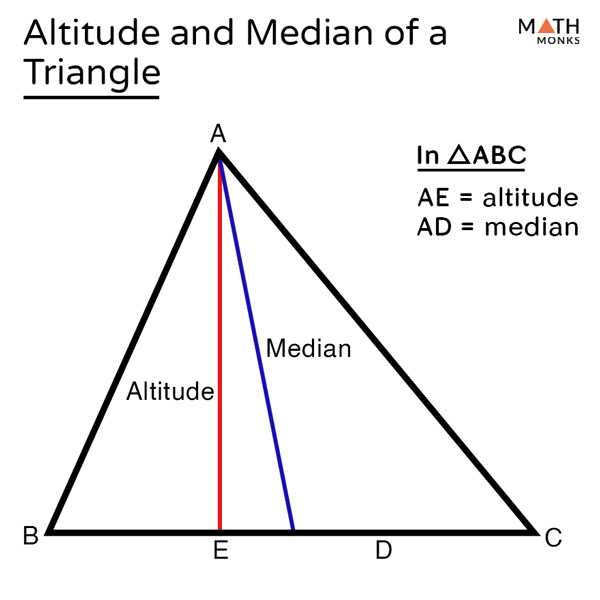
Yes, the altitude of a triangle is also referred to as the height of the triangle.A triangle is a polygon having 3 sides and three vertices. Is the Altitude of a Triangle Same as the Height of a Triangle? Since it is perpendicular to the base of the triangle, it always makes a 90° with the base of the triangle. Yes, the altitude of a triangle is a perpendicular line segment drawn from a vertex of a triangle to the base or the side opposite to the vertex. Does the Altitude of a Triangle Always Make 90° With the Base of the Triangle? It bisects the base of the triangle and always lies inside the triangle. The median of a triangle is the line segment drawn from the vertex to the opposite side that divides a triangle into two equal parts. It can be located either outside or inside the triangle depending on the type of triangle. The altitude of a triangle is the perpendicular distance from the base to the opposite vertex. The altitude of a triangle and median are two different line segments drawn in a triangle. What is the Difference Between Median and Altitude of Triangle? \(h= \frac\), where 'h' is the altitude of the scalene triangle 's' is the semi-perimeter, which is half of the value of the perimeter, and 'a', 'b' and 'c' are three sides of the scalene triangle. The following section explains these formulas in detail. The important formulas for the altitude of a triangle are summed up in the following table.

NAME AN ALTITUDE GEOMETRY HOW TO

Let us learn how to find out the altitude of a scalene triangle, equilateral triangle, right triangle, and isosceles triangle. Using this formula, we can derive the formula to calculate the height (altitude) of a triangle: Altitude = (2 × Area)/base. The basic formula to find the area of a triangle is: Area = 1/2 × base × height, where the height represents the altitude.